La dimostrazione di Griša

· by · in · 681 views
     

Il #thread che vi propongo oggi per la serie #PsychiatricStories è piuttosto lungo. Me ne scuso.

Qui l’indice.

1-10 Prologo
11-23 Personaggio
24-29 Conclusioni

Qui la raccolta di tutte le storie

https://www.ugoquinzi.it/category/cultura/scienza/psicologia/psychiatricstories/.

(1) Immaginate di bendare una formica e di farla camminare su un pallone di calcio. Poi, in rigoroso linguaggio formichiano, chiedetele di indicarvi la forma dell’oggetto sul quale sta camminando. Anche se togliete la benda alla formica, la poveretta non saprà cosa rispondervi.

(2) È più o meno lo stesso problema dei terrapiattisti, che a differenza della formica tengono la benda non davanti agli occhi ma davanti all’intelligenza. Un modo per sapere se la Terra è sferica (o quasi…) sarebbe di compiere una serie di cammini chiusi attorno a lei.

(3) Alla fine, stringendo sempre più i cammini, si arriverebbe ad un solo punto. Questa è la caratteristica di un oggetto sferico.

E se la Terra non fosse sferica? Sapete che per la geometria topologica (così si chiama questa scienza) non cambierebbe nulla se fosse piatta?

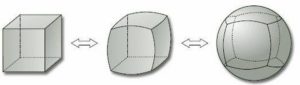(4) Cioè la Terra potrebbe essere conica, a parallelepipedo, cubica, purchè priva di buchi che la trapassino da parte a parte: per i matematici non cambierebbe nulla. Con arcane formule matematiche potrebbero stirarla, rigonfiarla, lisciarla e riportarla a sfera.

(5) Quello che per un comune mortale sembra un passatempo accademico, per un matematico è cibo della mente.

Ma… siamo davvero sicuri che tutti gli oggetti privi di buchi che li trapassino da parte a parte possano essere stirati, rigonfiati, lisciati e riportati a una sfera?

(6) Henri Poincaré se lo chiese nel 1904, ma non fu in grado di risolverlo.

Io ho esagerato nel semplificare un problema, restato senza soluzione per quasi 100 anni e conosciuto come Congettura di Poincaré, che @orporick saprà spiegarvi incommensurabilmente meglio di me.

(7) Perciò il prodigioso matematico terminò la presentazione della questione con una furbizia: “Questa questione ci porterebbe troppo lontano” e lasciò ai posteri l’incombenza di trovare il modo di stirare, rigonfiare, lisciare figure geometriche per farle diventare sfere.

(8) E di dimostrare che “ogni 3-varietà semplicemente connessa chiusa (ossia compatta e senza bordi) è omeomorfa a una sfera tridimensionale”. La cosa si rivelò così sfidante che nel 2000 la congettura fu inclusa tra i 7 problemi per il millennio.

http://www.claymath.org

(9) Anzi il Clay Institute offrì anche un premio di 1 milione di dollari per la sua soluzione. I problemi da superare però non erano pochi.

Prima occorreva individuare le singolarità che si sarebbero presentate durante l’operazione matematica di rigonfiamento.

(10) Poi era necessario scegliere il momento per rimodellare quelle singolarità.

Infine si doveva escludere che le operazioni chirurgiche di rimozione andassero avanti all’infinito.

Solo allora si poteva essere certi che l’oggetto matematico era destinato a diventare sfera.

(11) Il lungo prologo è stato necessario per far almeno intuire il grado di astrazione e la complessità del problema. Ora siamo al cuore della storia.

La dimostrazione della Congettura di Poincaré è riuscita ad un matematico russo, Grigorij Jakovlevič Perel’man detto Griša.

(12) Griša, nato nel 1966 a Leningrado, entrò giovanissimo nel club di Sergej Rukšin, un ristretto giro di brillanti menti che si preparavano a sostenere gare di matematica. Sergej intuì presto le potenzialità di Griša, che risolveva problemi 5 volte più velocemente di lui.

(13) Griša non sbagliava mai una dimostrazione, nemmeno in buona fede. Era onestissimo, Sergej diceva che “dimostrava una forma delirante di onestà“. Da professore di matematica una volta Griša ottenne una gratifica sullo stipendio. Si fece dire la somma esatta e la restituì.

(14) Se Griša dimostrava capacità non comuni nella matematica, dimostrava anche comportamenti curiosi, ai limiti del bizzarro, nella vita ordinaria. Era ossessivamente rispettoso delle regole e non si privava mai della compagnia e dell’accudimento della madre, anche da adulto.

(15) La madre, una matematica oppressa dal regime, seguiva molto Griša. In particolare chiese a Sergej di controllare che il figlio mangiasse e che si allacciasse le scarpe.

Ma fu una battaglia persa. Griša continuò a mangiare pochissimo e a girare con le scarpe slacciate.

(16) Il giovane Griša non si slegava mai il colbacco, nemmeno i paraorecchi, diceva che la madre lo avrebbe ucciso se l’avesse fatto. Leggeva poco spontaneamente, sosteneva che qualsiasi libro meritasse di essere letto si sarebbe dovuto inserire in un elenco obbligatorio.

(17) Griša rifiutava di lavarsi e persino di lavare i suoi panni sporchi. Da adulto poi si faceva crescere unghie e capelli in modo abnorme. Quando il suo mentore portava gli allievi a fare un bagno, Griša non entrava in acqua, stava a riva a contare le teste dei suoi compagni.

(18) Mentre risolveva problemi matematici Griša emetteva ululati o “terrore acustico“, come ricordano i compagni. Secondo lui canticchiava. Rifletteva facendo rimbalzare una pallina da ping-pong sul banco o passandosi le mani sui pantaloni fino a far diventare liscia la stoffa.

(19) Riuscì ad entrare all’Università vincendo le Olimpiadi della matematica del 1982 in Ungheria. Superò così lo scoglio più grande: l’ammissione al Mathmech pur essendo ebreo in una URSS antisemita. Tutto alla veneranda età di 16 anni!

Con la pubertà smise di farsi la barba.

(20) Dal 1991 al 1995 fu in USA. Il suo modo di insegnare e di spiegare in pubblico la soluzione di un problema era contorto. Tutti spiegano per farsi capire, Griša raccontava come si era relazionato al problema. Spesso in modo confuso, camminando avanti e indetro alla lavagna.

(21) Dal 1995 tornato in patria lavora all’Istituto Steklov senza far parlare di sé.

Ma il 12.11.2002 Griša invia una mail agli amici per annunciare di aver pubblicato su un sito specializzato un articolo altamente tecnico. È una sorpresa inaudita per la comunità matematica.

(22) L’anno successivo Griša pubblica altri due articoli, più brevi. In complessive 68 pagine geniali ha trovato la dimostrazione della Congettura di Poincaré, senza mai riconoscere di averlo fatto.

https://arxiv.org/find/math/1/au:+Perelman_Grisha/0/1/0/all/0/1?skip=0&query_id=2a3a7c7154578a2a

(23) Griša rifiuterà sia il premio da 1mln di dollari, sia la Medaglia Fields che gli sarà tributata nel 2006. Si dimette dal suo posto a Pietroburgo e si ritira in un modesto appartamento di periferia con la madre. Interrompe i contatti con il mondo e abbandona la matematica.

(24) Perché? Sono state avanzate tante ipotesi: rifiuto della competizione accademica, idealismo della visione scientifico-matematica, delusione da parte dei suoi colleghi, disgusto per gli interessi vili e per il denaro. La giornalista Masha Gessen ha una sua convinzione.

(25) Dopo aver raccolto centinaia di testimonianze e averle sottoposte a uno dei massimi esperti, Simon Baron-Cohen, è giunta alla conclusione che Grigorij Perel’man sia affetto da Sindrome di Asperger, disturbo delle spettro autistico che limita molto le competenze sociali.

(26) Pur tuttavia chi è affetto da Sindrome di Asperger sembra sviluppare altre competenze, al punto che non di rado esprime abilità geniali. Come Griša.

Ma la conclusione è legittima?

(27) La Gessen non ha mai incontrato Perel’man di persona; Griša non si lascia più vedere da nessuno da anni. Non è dato nemmeno di sapere se a Griša uno specialista abbia diagnosticato la Sindrome di Asperger né se qualcuno sia stato autorizzato a divulgare la diagnosi.

(28) A queste condizioni i dubbi sono più che motivati, per quanto la storia di Griša possa apparire simile a quella di tanti Asperger.

Due considerazioni finali. 1) Non affrettare mai i giudizi sui malati psichiatrici, possono rivelarsi geniali per aspetti negati ai più.

October 04,2011. St.Petersburg, Russia.
Pictured: Russian mathematician Grigori Perelman walking along Nevsky prospekt (avenue) of St.Petersburg. PhotoXPress

(29) 2) Grazie, Griša, per quello che hai fatto per l’umanità.

If you are reading this tweet: thank you, Griša, for your love of math and for your contribution in discovering the solution of the Poincaré Conjecture.

Potete leggere la storia di Griša anche su Twitter, seguendo il #thread.